Skip to main content

13 Floating Point

这篇笔记介绍lecture20、21，浮点数相关内容。

浮点数表示​

二进制​

与整数部分相同，浮点数二进制每一位也有相应的权重。整数部分存在overflow，浮点部分存在underflow。

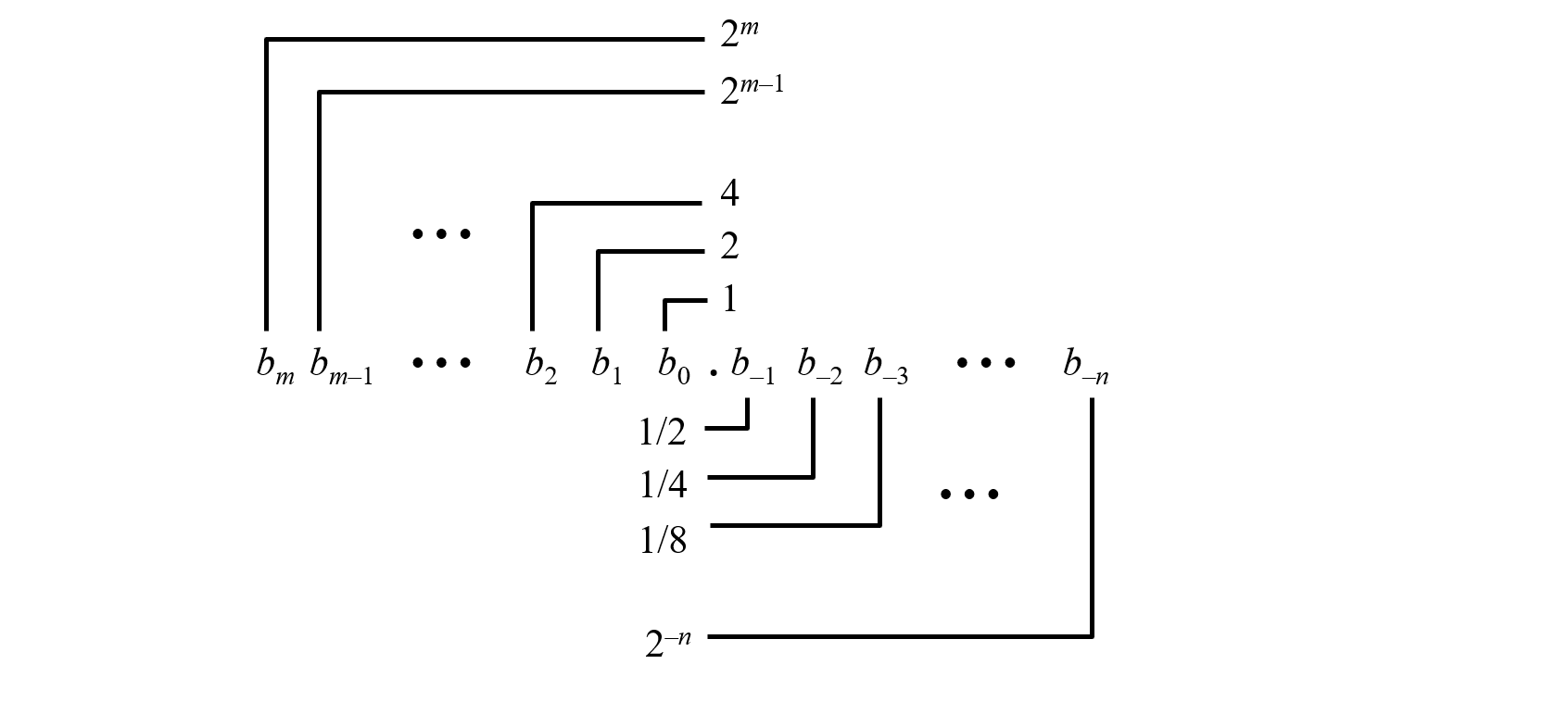
fraction binary number

将十进制整数部分转换为二进制需要除二取余，而将小数部分转为二进制需要乘二取整。例如，0.2的小数部分前八位是00110011。可以看出，二进制只能精确地描述 x/2kx/2^k ，其余都会不断循环。

IEEE​

IEEE浮点数的结构是

V=(−1)s×M×2EV = (-1)^s \times M \times 2^E

第一部分是符号位， ss 取0或1。第二部分是有效位（significand），是 [1.0,2.0)[1.0, 2.0) 间的一个值。第三部分是指数部分（exponent）。存储的排列顺序是S、E、M。

IEEE representation

暂不考虑指数位E全为0或全为1。此外，E并不是exp表示的值，而是 exp−biasexp - bias 。这里的bias是一个值，在单精度浮点数中为127，双精度中为1023，也就是 2m−12^m - 1 ， mm 是exp部分的位数。

由于实际的 MM 肯定是1.xxx，所以这个1不需要表示。

例如，12345的分数表示是 1.1000000111001×2131.1000000111001 \times 2^{13} ，16进制表示是 4640E4004640E400 。

以上的部分是normalized values，还有denormalized values。在 exp 为0时，EE与为1时同样视作-126，但是 MM 不再是1.xxx而是0.xxx，提供了更小的范围。当 exp 与 frac 均为0时，表示的数是0。

在 exp 为全1时，如果 frac 为0，则表示无穷大，符号与 SS 相同。如果 frac 不为0，表示NAN（not a number），出现在 sqrt(-1) 等情况中。更具体的NAN可以自定义。

分布与范围​

可以看出，指数位不同时，浮点数表示的精度不同。例如对于8位浮点数， exp 为0时两个相邻浮点数相隔 1/5121/512 ，而 exp 为1110（E为7）时两个相邻浮点数相差16（ 2−3×272^{-3} \times 2^7 ）。越靠近0，浮点数的分布就越密。

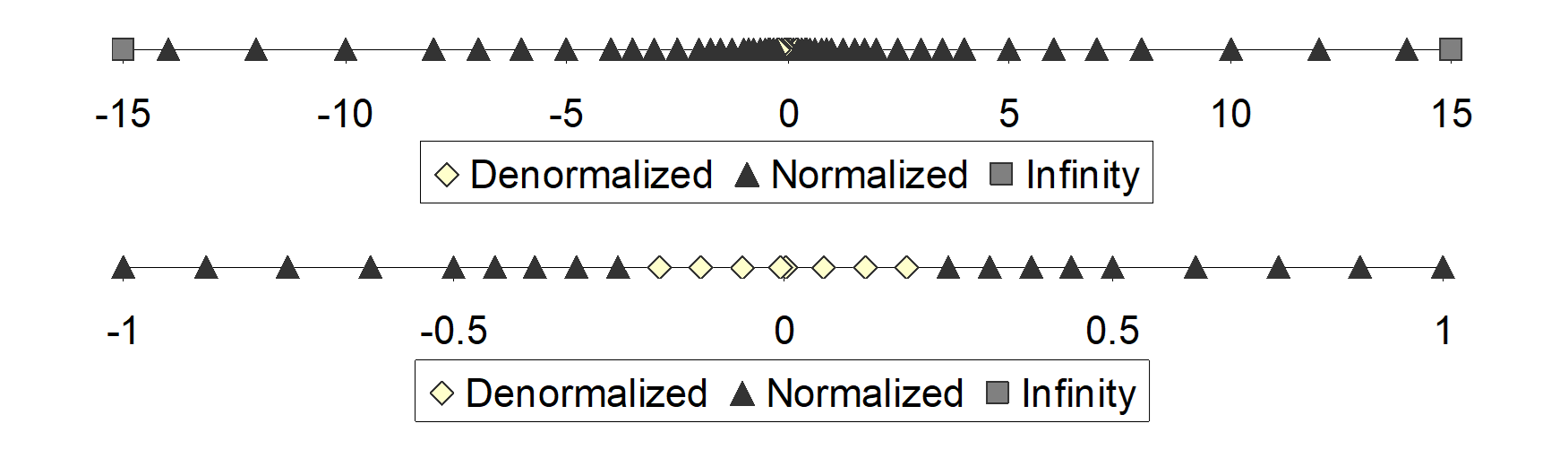
dynamic range

此外，一些相关数值如下图。

interesting numbers

浮点数运算​

Rounding Mode​

一共有四种rouding mode。

Round-down指结果不会大于原值，round-up指结果不会小于原值，round-toward-zero指结果尽量靠近0。对于round-to-even，在需要舍去的位不为5时，与常规四舍五入相同；在需要舍去的位为5时，使结果为偶数。

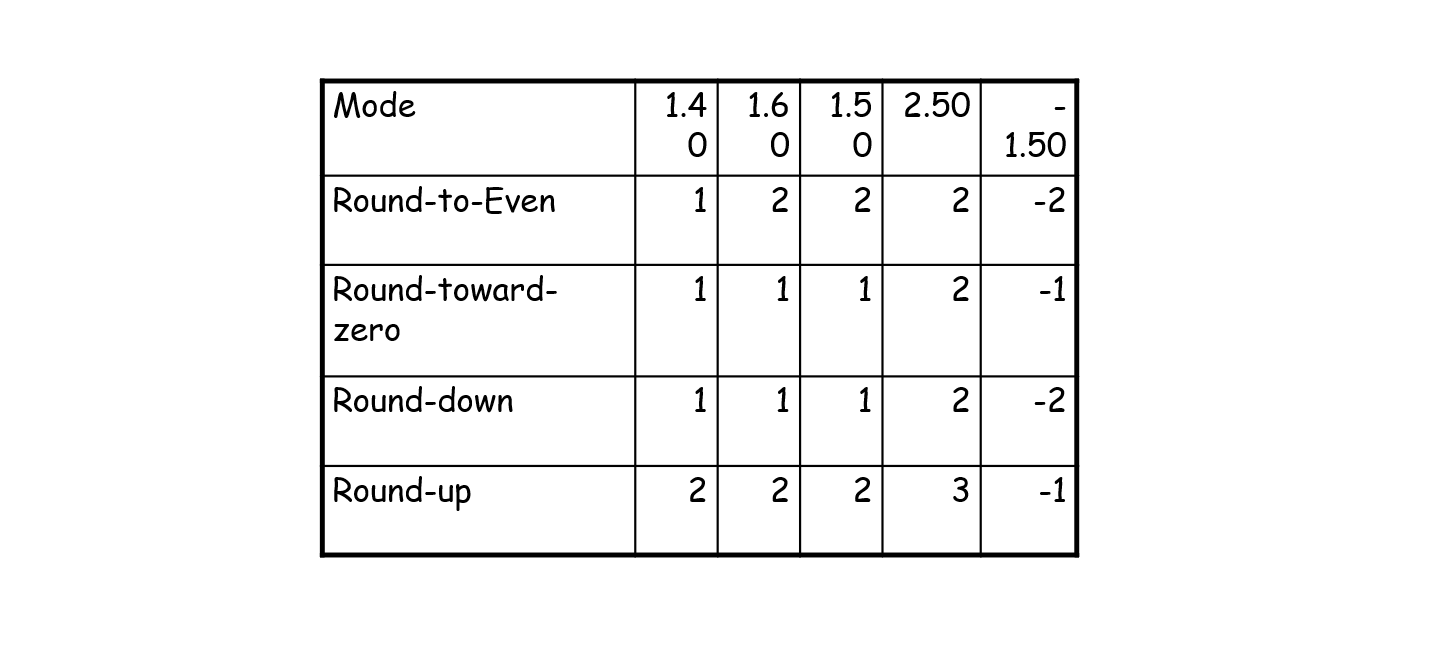
rounding mode

一般来说采用round-to-even模式。对于二进制，四舍五入时使得最后一个有效位为0。

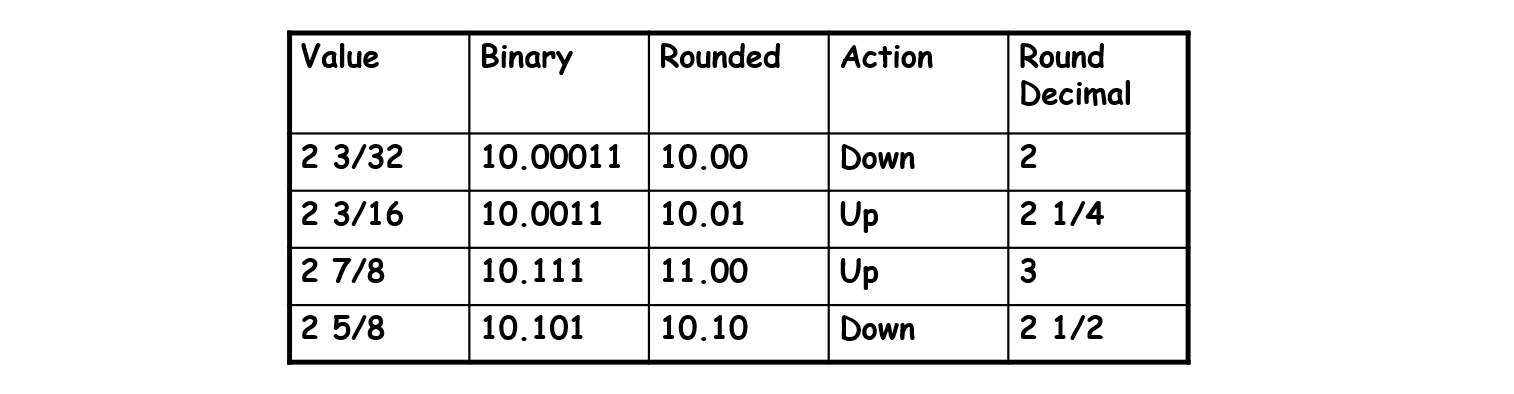
round to even

乘法​

浮点数乘法的思路是先算出精确值，让后将它改为合适的IEEE浮点数。

对于浮点数 (−1)s1 M1 2E1(-1)^{s1}~M1~2^{E1} 和 (−1)s2 M2 2E2(-1)^{s2}~M2~2^{E2} ，符号位精确值是 s1 ˆ s2s1~\^{}~s2 ， 有效位精确值是 M1×M2M1 \times M2 ，指数位精确值是 E1+E2E1 + E2 。

如果M大于等于2，将其右移并增加E，然后调整M使其符合对应的表示。

加法​

对于浮点数 (−1)s1 M1 2E1(-1)^{s1}~M1~2^{E1} 和 (−1)s2 M2 2E2(-1)^{s2}~M2~2^{E2} ，假设 E1>E2E1 > E2 。

将第二个浮点数对应的有效位右移，然后和第一个数相加。将相加后的M左移/右移至相应位置，处理s的值，调整M round to even。

Puzzles​

floating point puzzles

可以看到浮点数不符合结合律。

另外，浮点数转为整数时会将小数部分截掉，超出整数范围时会出现未定义操作。int转为double是精确的，转为float可能导致精度损失，因为int能表达的最大整数是 232−12^32 - 1 ，而float为 224−12^24 - 1 。

浮点汇编​

寄存器​

共有16个YMM寄存器，为256位，后128位为XMM寄存器。浮点指令只使用低阶32位（float）或64位（double）。

前八个XMM寄存器（%xmm0~%xmm7）可用于传递参数，多余的参数放到栈上。函数的返回值存储在%xmm0。所有xmm寄存器均为调用者保存。参数包含各种数据类型时，根据它们的类型决定使用的寄存器；例如在函数 double f(int x, double y, long z) 中， x 存储在%edi， y 存储在%xmm0， z 存储在 %rsi。

寄存器​

移动指令如下图，其中Mi代表内存中i位。

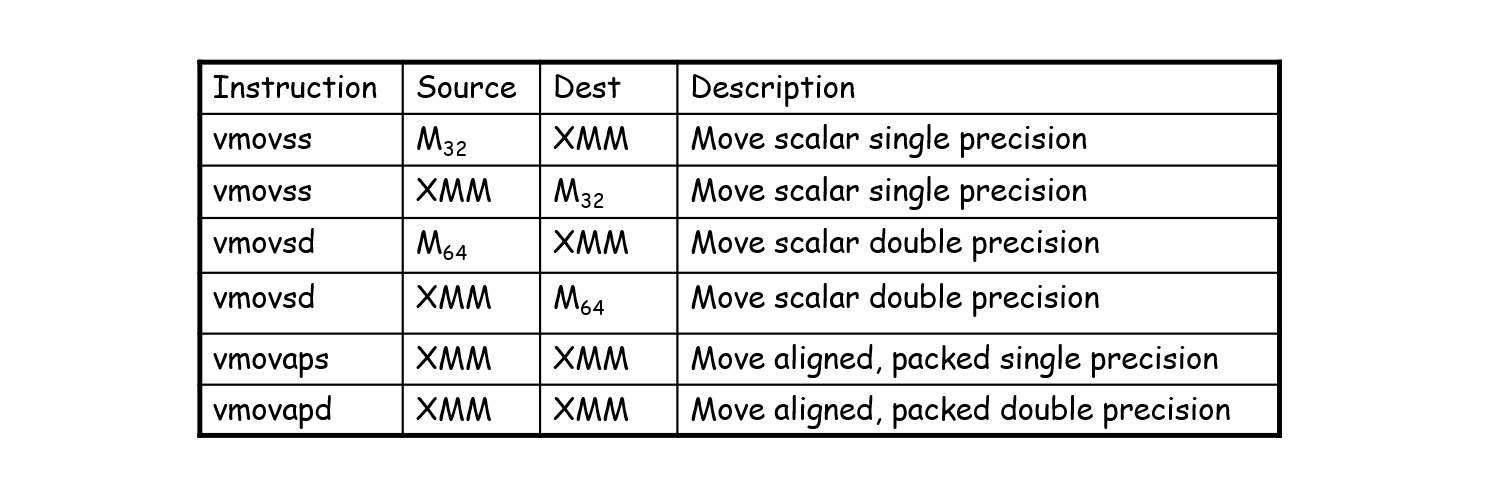
FP move

此外还有数据类型转换的指令。

下图中round to zero。

FP to int

下图中将int转为浮点数。虽然是三操作数指令，但是第二个操作数被忽略。

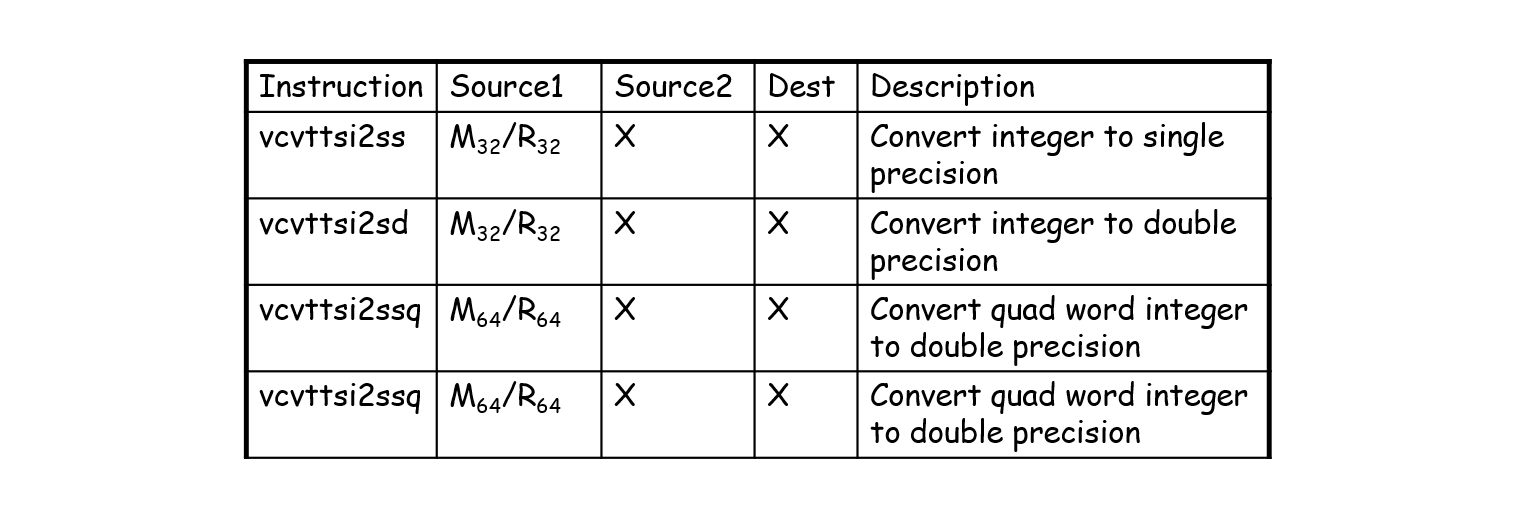
int to FP

以下三张图分别是算数运算、逻辑运算和比较。

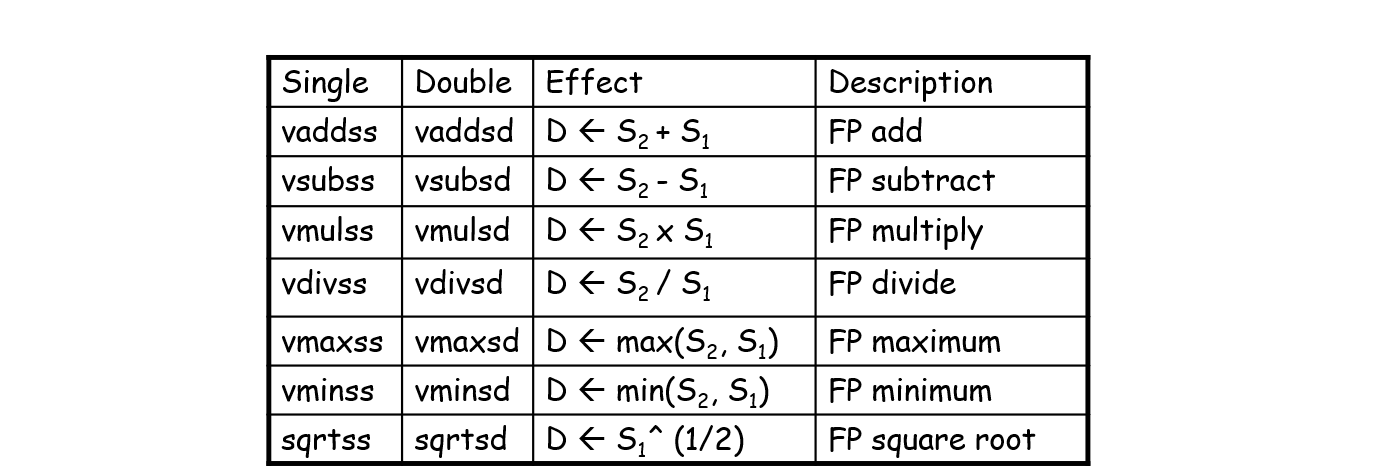
FP arithmetic operations

FP logical operations

FP comparision operations

此外，浮点中没有立即数。系统会为浮点常量分配空间并初始化，放在只读部分中（类似字符串）。